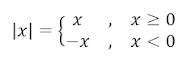A. Definisi Nilai Mutlak
Nilai mutlak suatu bilangan real x didefinisikan sebagai:
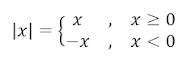
Contoh 1:1. |5| = 5
2. |0| = 0
3. |-4|= -(-4) = 4
Perlu diperhatikan bahwa tidak dapat kita katakan bahwa |-x| = x, contohnya dengan mengambil x = -8, maka |-(-8)| ¹ -8
B. Sifat-sifat Nilai Mutlak
Misalkan x, y, dan a adalah bilangan real dengan a > 0, maka
Catatan: Berdasarkan sifat 10, yaitu |x| £ a Û -a £ x £ a diperoleh
|x - c| < a Û -a+ c < x < a+ c.
Contoh 2:
Carilah himpunan penyelesian dari pertaksamaan berikut:
a. |x +1| £ 4
b. |2x - 7| < 3
c. |x - 2| < 3|x+7|
d. |2+5/x| > 1
Penyelesaian:
a. |x +1| £ 4 Û -4 £ x +1 £ 4 (Sifat 10)
Û -5 £ x £ 3
jadi, Hp = {xÎR| -5 £ x £ 3}= [-5,3]
Cara lain:
|x +1| £ 4 Û (x +1)2 £ 16 (Sifat 10)
Û x2+2x +1£ 16
Û x2+2x -15 £ 0
Titik-titik pemecah pertaksamaan kuadrat di atas adalah -5 dan 3, titik-titik pemecah tersebut membagi garis bilangan menjadi tiga selang/interval yaitu (-¥,-5), (-5,3), dan (3,¥).
jadi, Hp = {xÎR| -5 £ x £ 3}= [-5,3]
Dengan definisi nilai mutlak:
|x +1| = x+1, jika x ³ -1 sehingga x+1 £ 4 Û x £ 3
|x +1| = -(x+1), jika x < -1 sehingga -x - 1 £ 4 Û x ³ -5



jadi, Hp = {xÎR| -5 £ x £ 3}= [-5,3]
b. |2x - 7| < 3 Û -3 < 2x -7 < 3 (Akibat sifat 10)
Û 4 < 2x < 10 Û 2 < x < 5
jadi, Hp = {xÎR| 2 < x < 5}= [-5,3]
Cara lain:
|2x - 7| < 3 Û (2x -7)2 < 9 (Akibat sifat 10)
Û 4x2-28x +49 < 9
Û 4x2-28x +40 < 0
Û x2-7x +10 < 0
Titik-titik pemecah pertaksamaan kuadrat di atas adalah 2 dan 5, titik-titik pemecah tersebut membagi garis bilangan menjadi tiga selang/interval yaitu (-¥,2), (2,5), dan (5,¥).
jadi, Hp = {xÎR| 2 < x < 5}= (2,5)
Dengan definisi nilai mutlak:
|2x - 7| = 2x-7, jika x ³ 7/2 sehingga 2x-7 < 3 Û x < 5
|x +1| = -(2x-7), jika x < 7/2 sehingga -2x + 7 < 3 Û x > 2
jadi, Hp = {xÎR| 2 < x < 5}= (2,5)
c. |x - 2| < 3|x+7| Û |x - 2| < |3||x+7| (Definisi nilai mutlak)
Û |x - 2| < |3(x+7)| (Sifat 7) Û |x - 2| < |3x+21|
Û (x - 2)2 < (3x+21)2 (Sifat 12)
Û x2-4x+4 < 9x2+126x+441
Û 8x2+130x+437 > 0
Û (x+23/2)(x+19/4) > 0
Titik-titik pemecah pertaksamaan kuadrat di atas adalah -23/2 dan -19/4, titik-titik pemecah tersebut membagi garis bilangan menjadi tiga selang/interval yaitu (-¥,-23/2), (-23/2,-19/4), dan (-19/4,¥).
jadi, Hp = {xÎR| 2 < x < 5}= (2,5)
Dengan definisi nilai mutlak:
|x - 2| = x - 2, jika x ³ 2 dan |x + 7| = x + 7, jika x ³ -7
|x - 2| = -(x - 2), jika x < 2 |x + 7| = -(x + 7), jika x < -7
x - 2 < 3(x + 7) x - 2 < 3(-(x + 7))
Û x - 2 < 3x + 21 Û x - 2 < -3x - 21
Grafik pada garis bilangannya adalah:


selang (-23/2 , -19/4) tidak memenuhi
-(x - 2) < 3(x + 7) -(x - 2) < 3(-(x + 7))
Û -x + 2 < 3x + 21 Û -x + 2 < -3x - 21
Grafik pada garis bilangannya adalah:


jadi, Hp = {xÎR| x < -23/2 atau x > -19/4}
d. |2+5/x| > 1
Û 2+5/x > 1 atau 2+5/x < -1 (Akibat sifat 11)
Û (2x+5)/x > 1 atau (2x+5)/x < -1
Û (2x+5)/x - 1 > 0 atau (2x+5)/x + 1 < 0
Û (x+5)/x > 0 atau (3x+5)/x < 0
Perhatikan bentuk (x+5)/x > 0
Titik-titik pemecah pertaksamaan kuadrat di atas adalah -5 dan 0, maka terdapat tiga selang/interval yaitu (-¥,-5), (-5,0), dan (0,¥).
u artinya tidak terdefinisi pada x = 0
sehingga {xÎR| x < -5 atau x > 0}= (-¥,-5) È (0,¥)
Titik-titik pemecah pertaksamaan kuadrat di atas adalah -5/3 dan 0, maka terdapat tiga selang/interval yaitu (-¥,-5/3), (-5/3,0), dan (0,¥).
sehingga {xÎR| -5 < x < 0}= (-5/3,0)
jadi, Hp = {xÎR| x < -5 atau -5/3 < x < 0 atau x > 0}
= (-¥,-5) È (-5/3,0) È (0,¥)