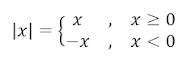Matematika Diskret

Matematika Diskret (Discrete Mathematics) merupakan cabang ilmu matematika yang mempelajari tentang objek-objek diskret. Sebelum masuk lebih dalam tentang matematika diskret diharapkan pelajar sudah memahami mengenai logika dan himpunan. Adapun materi dalam pembahasan matematika diskret ini adalah sebagai berikut:

1. Pencacahan/Perhitungan
2. Permuasi dan Kombinasi
3. Aljabar Boolean
4. Teori bilangan dan kriptografi
5. Bilangan Prima dan Pembagian Bersama Terbesar
6. Graf
7. Gerbang Logika

Materi:

P01    :    Kontrak Kuliah dan Pengantar Mata Kuliah.

P02    :    Perhitungan (Counting).

P03    :    Prinsip Sarang Merpati dan Perumumannya.

P04    :    Permutasi dan Kombinasi.

P05    :    Generalisasi Permutasi dan Kombinasi.

P06    :    Koefisien dan Identitas Binomial

P07    :    Aljabar Boolean.

P08    :    Ujian Tengah Semester (UTS)

P09    :    Keterbagian dan Aritmatika Modulo.

P10    :    Representasi Bilangan Bulat.

P11    :    Bilangan Prima dan Pembagian Bersama Terbesar.

P12    :    Graf: Graf dan Model Graf, Terminologi Graf, dan Jenis Graf Khusus.

P13    :    Graf: Representasi Graf, Graf Isomorfisme, dan Konektivitas.

P14    :    Gerbang Logika: Jenis Gerbang Dasar dan Kombinasi Gerbang.

P15    :    Gerbang Logika: Penambah dan Peminimalan Sirkuit.

Referensi:

v  Rossen, Kenneth H. (2019). Discrete Mathematics and Its Applications Eighth Edition. New York, McGraw-  Hill

v  Bona, Miklos (2022). Combinatorics of Permutations. New York, Chapman & Hall

v  Bierbrauer, Jurgen (2017). Introduction to Coding Theory, Second Edition. New York, Chapman & Hall.

Statistika Matematika

Statistika Matematika (Mathematical Statistics) merupakan terapan matematika pada statistika. teknik matematika yang digunakan meliputi probabilitas, permutasi dan kombinasi, fungsi dan grafiknya, integral, aljabar, dan sebagainya. Dalam pembahasannya statistika matematika dipisahkan menjadi dua yaitu Stastistika Matematika I dan Stastistika Matematika II. Fokus pembahasan ini adalah Statistika matematika I yang memuat pokok bahasan sebagai berikut:

1. Konsep Dasar Peluang
2. Peubah Acak dan Distribusi Peluangnya
3. Ekspektasi Matematika
4. Beberapa Distribusi Peluang Diskret
5. Beberapa Distribusi Peluang Kontinu

Materi:

P01    :    Pengantar Statistika Matematika.

P02    :    Ruang Sampel, Kejadian, dan Menentukan Banyaknya Titik Sampel.

P03    :    Peluang suatu Kejadian, Aturan Penjumlahan, dan Peluang Bersyarat.

P04    :    Kejadian Bebas, Aturan Perkalian, Aturan Penghapusan, dan Aturan Bayes.

P05    :    Definis Peubah Acak, Jenis-jenis Peubah Acak, Distribusi Peluang Diskret, 

                dan Distribusi Peluang Kontinu.

P06    :    Distribusi Peluang Gabungan

P07    :    Rataan, Variansi dan Kovariansi Peubah Acak.

P09    :    Rataan dan Variansi dari Kombinasi Linear Peubah Acak, dan Teorema

               Chebyshev.

P10    :    Distribusi Seragam Diskret, Binomial dan Multinomial.

P11    :    Distribusi Hipergeometrik, Binomial Negatif, Geometrik dan Poisson.

P12    :    Distribusi Normal, Luas di Bawah Kurva Normal, Penerapan Distribusi Normal.

P13    :    Hampiran Normal terhadap Binomial, Distribusi Gamma dan Eksponensial.

P14    :    Kaitan Distribusi Gamma dan Eksponensial dengan Proses Poisson, Penerapan Distribusi Gamma dan Eksponensial.

P15    :    Distribusi Khi-Kuadrat dan Weibull.

Referensi:

Walpole, Ronald E. and Myers, Raymond H. (1995). Ilmu Peluang dan Statistika untuk Insinyur dan Ilmuwan. Edisi ke-4. Bandung: ITB Bandung.

Nilai Mutlak

 

A.  Definisi Nilai Mutlak

Nilai mutlak suatu bilangan real x didefinisikan sebagai:

 

Contoh 1:

1.    |5| = 5

2.    |0| = 0

3.    |-4|= -(-4) = 4

Perlu diperhatikan bahwa tidak dapat kita katakan bahwa |-x| = x, contohnya dengan mengambil x = -8, maka |-(-8)| ¹ -8

B.  Sifat-sifat Nilai Mutlak

Misalkan x, y, dan a adalah bilangan real dengan a > 0, maka

Catatan: Berdasarkan sifat 10, yaitu |x| £ a Û -a £ x £ a diperoleh 

         |x - c| < a Û -a+ c < x < a+ c.

Contoh 2:

Carilah himpunan penyelesian dari pertaksamaan berikut:

a.    |x +1| £ 4

b.    |2x - 7| < 3

c.    |x - 2| < 3|x+7|

d.    |2+5/x| > 1

Penyelesaian:

a.     |x +1| £ 4    Û -4 £ x +1 £ 4        (Sifat 10)

                           Û -5 £ x £ 3    

        

        jadi, Hp = {xÎR| -5 £ x £ 3}= [-5,3]

        Cara lain:

        |x +1| £ 4    Û (x +1)² £ 16        (Sifat 10)

                           Û x²+2x +1£ 16

                              Û x²+2x -15 £ 0

                              Û (x+5)(x-3) £ 0

Titik-titik pemecah pertaksamaan kuadrat di atas adalah -5 dan 3, titik-titik pemecah tersebut membagi garis bilangan menjadi tiga selang/interval yaitu (-¥,-5), (-5,3), dan (3,¥). 

         jadi, Hp = {xÎR| -5 £ x £ 3}= [-5,3]

         Dengan definisi nilai mutlak:

        

        |x +1| = x+1, jika  x ³ -1  sehingga x+1 £ 4 Û x £ 3

        |x +1| = -(x+1), jika  x < -1  sehingga -x - 1 £ 4 Û x ³ -5

 

        jadi, Hp = {xÎR| -5 £ x £ 3}= [-5,3]

b.     |2x - 7| < 3      Û -3 < 2x -7 < 3        (Akibat sifat 10)

                               Û 4 < 2x < 10  

                                   Û 2 < x < 5  

        

        jadi, Hp = {xÎR| 2 < x < 5}= [-5,3]

        Cara lain:

        |2x - 7| < 3  Û (2x -7)² < 9            (Akibat sifat 10)

                           Û 4x²-28x +49 < 9

                              Û 4x²-28x +40 < 0

                              Û x²-7x +10 < 0

                              Û (x-2)(x-5) < 0

Titik-titik pemecah pertaksamaan kuadrat di atas adalah 2 dan 5, titik-titik pemecah tersebut membagi garis bilangan menjadi tiga selang/interval yaitu (-¥,2), (2,5), dan (5,¥).  

         jadi, Hp = {xÎR| 2 < x < 5}= (2,5)

         Dengan definisi nilai mutlak:

        

        |2x - 7| = 2x-7, jika  x ³ 7/2  sehingga 2x-7 < 3 Û x < 5

        |x +1| = -(2x-7), jika  x < 7/2  sehingga -2x + 7 < 3 Û x > 2 

        jadi, Hp = {xÎR| 2 < x < 5}= (2,5)

c.     |x - 2| < 3|x+7|    Û |x - 2| < |3||x+7|                (Definisi nilai mutlak)

                                   Û |x - 2| < |3(x+7)|             (Sifat 7)

                                       Û |x - 2| < |3x+21|       

                                   Û (x - 2)² < (3x+21)²         (Sifat 12)

                                       Û x²-4x+4 < 9x²+126x+441

                                       Û 8x²+130x+437 > 0

                                       Û (x+23/2)(x+19/4) > 0

        

Titik-titik pemecah pertaksamaan kuadrat di atas adalah -23/2 dan -19/4, titik-titik pemecah tersebut membagi garis bilangan menjadi tiga selang/interval yaitu (-¥,-23/2), (-23/2,-19/4), dan (-19/4,¥). 

         jadi, Hp = {xÎR| 2 < x < 5}= (2,5)

         Dengan definisi nilai mutlak:

        

        |x - 2| = x - 2, jika  x ³ 2        dan        |x + 7| = x + 7, jika x ³ -7

        |x - 2| = -(x - 2), jika  x < 2                  |x + 7| = -(x + 7), jika x < -7 

Dengan demikian, 

     x - 2 < 3(x + 7)                      x - 2 < 3(-(x + 7))  

Û x - 2 < 3x + 21                  Û x - 2 < -3x - 21  

Û 2x > -23                            Û 4x < -19

Û x > -23/2                           Û x < -19/4

Grafik pada garis bilangannya adalah:

selang (-23/2 , -19/4)  tidak memenuhi 

    -(x - 2) < 3(x + 7)                      -(x - 2) < 3(-(x + 7)) 

Û -x + 2 < 3x + 21                  Û -x + 2 < -3x - 21

Û 4x > -19                               Û 2x < -23

Û x > -19/4                              Û x < -23/2 

 Grafik pada garis bilangannya adalah:

        jadi, Hp = {xÎR|  x < -23/2  atau   x > -19/4}

    = (-¥,-23/2) È (-19/4,¥)

 

d.     |2+5/x| > 1  

        Û 2+5/x > 1    atau  2+5/x < -1                (Akibat sifat 11)

        Û (2x+5)/x > 1    atau  (2x+5)/x < -1                

        Û (2x+5)/x - 1 > 0    atau  (2x+5)/x + 1 < 0                

        Û (x+5)/x > 0    atau  (3x+5)/x < 0                

                                       

         Perhatikan bentuk (x+5)/x > 0

Titik-titik pemecah pertaksamaan kuadrat di atas adalah -5 dan 0, maka terdapat tiga selang/interval yaitu (-¥,-5), (-5,0), dan (0,¥). 

         u artinya tidak terdefinisi pada x = 0

         sehingga {xÎR|  x < -5 atau x > 0}= (-¥,-5) È (0,¥)

         Bentuk (3x+5)/x < 0

Titik-titik pemecah pertaksamaan kuadrat di atas adalah -5/3 dan 0, maka terdapat tiga selang/interval yaitu (-¥,-5/3), (-5/3,0), dan (0,¥).

         sehingga {xÎR|  -5 < x < 0}= (-5/3,0) 

jadi, Hp = {xÎR|  x < -5  atau -5/3 < x < 0  atau  x > 0}

                       = (-¥,-5) È (-5/3,0) È (0,¥)

        

Peluang Kejadian dan Bersyarat

A. Peluang suatu kejadian

Definisi 1.1: Peluang suatu kejadian A, dinyatakan dengan P(A) adalah jumlah bobot semua titik sampel yang termasuk A. jadi:

a)    0  P(A)  1

b)    P() = 0, dan

c)    P(T) =1

Contoh 1.1:

Sebuah mata uang logam dilantunkan dua kali. Berapakah peluangnya paling sedikit muncul muka sekali?

Penyelesaian:

Ruang sampel percobaan ini adalah

    T = { MM, MB, BM, BB}

Diasumsikan mata uang tersebut setangkup, maka tiap hasil mempunyai kemungkinan kemunculan yang sama.

Karena itu, setiap titik sampel diberi bobot b, sehingga 4b =1 atau b = 1/4. Jika A menyatakan kejadian bahwa paling sedikit muncul muka sekali, yaitu
    A = {MM, MB, BM}
Maka
    P(A) = 1/4+1/4+1/4 = 3/4.

Contoh 1.2:

Suatu dadu dibuat sedemikian rupa sehingga kemungkinan muncul suatu angka genap dua kali lebih besar daripada kemungkinan muncul angka ganjil. Jika K menyatakan kejadian munculnya suatu angka yang lebih besar dari 4 dalam sekali lantunan, hitunglah P(K)!

Penyelesaian:

Rungan sampel dadu sekali lantunan adalah
    T = {1, 2, 3, 4, 5, 6}

Misalkan bobot setiap titik sampel bernomor ganjil adalah b, maka bobot angka genap sebesar 2b, sehingga 9b = 1 atau b = 1/9. Kejadian K adalah
    K = {5, 6}
Dengan demikian,
    P(K) = 1/9+2/9 = 3/9 = 1/3.

Materi lebih lanjut dapat dilihat pada file pdf berikut: